Calculation of support reactions of a beam
Problem 4-1
Find the reactions at the support of the following beam shown in figure 4-1(a).
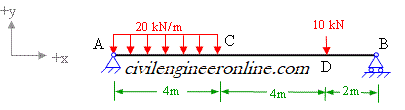
Figure 4-1(a)
Solution:
The given beam is considered as 2-dimensional structure. The free-body diagram of the beam is given in figure 4-1 (b) which shows all the reaction components (Ax, Ay, By) and the applied loads. This beam is statically determinate as it can have only 3 reaction components; 2 at the hinged support at A and 1 at the roller support at B, and there are 3 possible equations of static equilibrium ΣFx = 0, ΣFy = 0, ΣMz = 0; (The x-axis and y-axis are as shown in the figure and the z-axis is perpendicular to the x-y plane.)
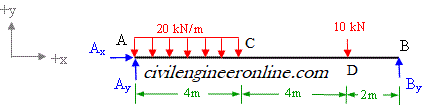
Figure 4-1(b) free-body diagram
Applying equations of static equilibrium:
ΣFx = 0; Ax = 0; (eq. 1)
ΣFy = 0; Ay + By 10 20 × 4 = 0;
Ay + By = 90 kN; (eq. 2)
Considering z-axis passing through A, and taking moment of all the forces about z-axis (taking clockwise ve and anticlockwise +ve);
ΣMz = 0; By × 10 -10 × 8 20 × 4 × 2 = 0 (eq. 3)
Solving eq. 3 yields By = 24 kN;
Substituting the value of By in eq. 4-2 gives Ay = 66 kN.
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Containing Tall buildings worldwide
Forthcoming conferences
Containing List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
PleaseTell your Friends about us if you find our website useful