Slope and deflection calculation by unit load method
Problem 7-3
Use unit load method to find the deflection at the center of the beam shown in figure 7-3(a). Take E= 200 GPa and I=400x106 mm4
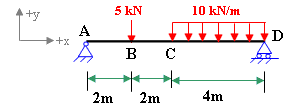
Figure 7-3(a)
Solution:
In the case of unit load method the deflection at a point of beam is given as
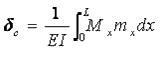
To write the equations of bending moment for different parts of the beam we have to first calculate the support reactions by applying the equations of equilibrium
(i) reactions due to actual loading
Ay = 13.75 kN; Dy = 31.25 kN
write the equations of bending moment for different part of the beam (origin of axes at A).
Mx = 13.75x ; (0 ≤ x ≤ 2)
Mx = 13.75x - 5(x-2) ; (2 ≤ x ≤ 4)
Mx = 13.75x - 5(x-2) -10(x-4)(x-4)/2; (4 ≤ x ≤ 8)
(ii) reactions due to virtual unit load at C
ay = 0.5 kN; by = 0.5 kN
mx = 0.5x (0 ≤ x ≤ 4)
mx = 0.5x - 1(x-4) (4 ≤ x ≤ 8)
Depending upon the validity of different bending moment equations, the deflection at point C can be written as follows;
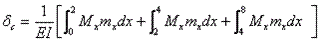
substituting the appropriate bending moment equations for Mx and mx
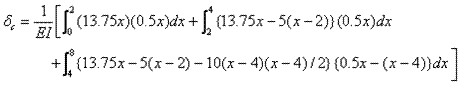
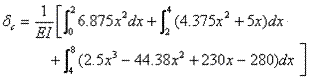
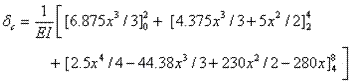
δc = 302.58 kN.m3/EI
substituting the values of E I in the above expression we get;
δc = (302.58 kN.m3)/{(200*106kN/m2)(400*10-6m4)}
δc = 0.0038 m = 3.8 mm
You can also use our deflection calculator to solve this problem
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Containing Tall building worldwide
Forthcoming conferences
Containing List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
PleaseTell your Friends about us if you find our website useful