Solving indeterminate frame by moment distribution method
Problem 8-2
Use Moment distribution method to find the resultant end moments for the non-sway frame shown in figure 8-2(a). Also draw bending moment diagram. Take EI as constant for all the members of the frame.
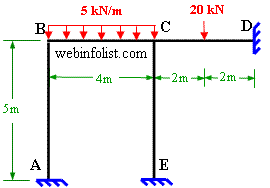
Figure 8-2(a)
Solution:
Step 1: The given rigid frame is non-sway because of lateral support at D. Consider each span (AB, BC, CD and CE) with both ends fixed and calculate the fixed-end moments as follows;
MAB = 0
MBA = 0
MBC = wL2 /12 = -6.67 kNm
MCB = -wL2 /12 = +6.67 kNm
MCD = PL/8 = -10 kNm
MDC = -PL/8 = +10 kNm
MCE = 0
MEC = 0
Step 2: Stiffness Coefficients
kAB = 4EI/L = 4EI/5 = 0.8EI
kBA = 4EI/L = 4EI/5 = 0.8EI
kBC = 4EI/L = 4EI/4 = EI
kCB = 4EI/L = 4EI/4 = EI
kCD = 4EI/L = 4EI/4 = EI
kDC = 4EI/L = 4EI/4 = EI
kCE = 4EI/L = 4EI/5 = 0.8EI
kEC = 4EI/L = 4EI/5 = 0.8EI
Step 3: Distribution factors
DAB = 0 (fixed support at the end)
DBA = 0.8EI/(0.8EI+EI) = 0.44
DBC = EI/(0.8EI+EI) = 0.56
DCB = EI/(EI+EI+0.8EI) =0.36
DCD = EI/(EI+EI+0.8EI) = 0.36
DCE = 0.8EI/(EI+EI+0.8EI) = 0.28
DDC = 0 (fixed support at the end)
DEC = 0 (fixed support at the end)
Calculation for moment distribution is shown in a systematic way in a tabular form. Each joint is balanced by distributing the unbalanced moment into the connected members in proportion of distribution factors. These calculation steps for balancing of joints are shown with grey colour to show the illustration. The carry-over moments (half of the balancing moment at near end) are applied on the far end, e.g. carry-over half of the balancing moment from BA to AB, BC to CB, CB to BC, CD to DC and CE to EC etc.
(In case of mobile device please scroll horizontally to view the full width of table)
| Table for Moment Distribution | ||||||||
| Joints |
A |
B |
C |
D | E | |||
| Members |
AB |
BA |
BC |
CB |
CE |
CD |
DC |
EC |
| Distribution Factors | 0 | 0.44 | 0.56 | 0.36 | 0.28 | 0.36 | 0 | 0 |
| Initial Fixed-end Moments | 0 | 0 | -6.67 | +6.67 | 0 | -10 | +10 | 0 |
| Balancing |
6.67x0.44 2.94 |
6.67x0.56 3.74 |
+3.33x0.36 1.2 |
+3.33x0.28 0.93 |
+3.33x0.36 1.2 |
|||
| Carry-over | 1.47 | 0.6 | 1.87 | 0.6 | 0.47 | |||
| Balancing |
-0.6x0.44 -0.264 |
-0.6x0.56 -0.336 |
-1.87x0.36 -0.67 |
-1.87x0.28 -0.52 |
-1.87x0.36 -0.67 |
|||
| Carry-over | -0.132 | -0.33 | -0.168 | -0.33 | -0.26 | |||
| Balancing |
0.33x0.44 0.145 |
0.33x0.56 0.185 |
0.168x0.36 0.06 |
0.l68x0.28 0.048 |
0.168x0.36 0.06 |
|||
| Carry-over | 0.072 | 0.03 | 0.092 | 0.03 | 0.024 | |||
| Balancing |
-0.03x0.44 -0.013 |
-0.03x0.56 -0.017 |
-0.092x0.36 -0.033 |
-0.092x0.28 -0.026 |
-0.092x0.36 -0.033 |
|||
| Carry-over | -0.006 | -0.016 | -0.008 | -0.016 | -0.013 | |||
| Final End-Moments | 1.41 | 2.83 | -2.83 | 8.98 | 0.51 | -9.49 | 10.26 | 0.26 |
Resultant bending moment diagram in figure 8-2(b) is plotted by superposing the span moment diagram and support moment diagram.
Note: Please use our bending moment calculator to get the values of span moments
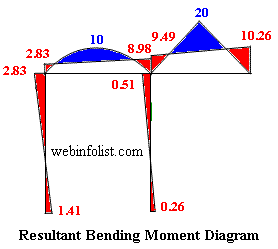
(all values in kNm)
(span moment in blue colour, support moment in red colour
Figure 8-2(b)
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Contining Tall building worldwide
Forthcoming conferences
Contining List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
PleaseTell your Friends about us if you find our website useful