Method of Virtual Work (Unit Load Method) for slope and deflection

Unit load method also referred to as method of virtual work was developed by John Bernoulli in 1717. It is used to determine the slope and deflection at a specified point of a beam, frame, or truss.

In this method a virtual unit load is applied at the point of deflection (δ) and in the direction of deflection, whereas a unit virtual moment is applied at the point of desired slope.

By applying the principle of work and energy we get

external virtual work = internal virtual work

External virtual work =1kN.δ

Therefore, δ = Internal virtual work

Based on internal virtual work for different types of loading the deflection formula is given as follows;

 

Flexural members

In case of flexural members (beam, frame) the total internal virtual work is obtained by integration.

  

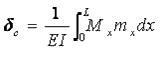
Where δ = deflection at point C

M_x = bending moment at x due to actual loading

m_x = bending moment at x due to virtual unit load applied at point of deflection, C.

L = beam span

E = Modulus of elasticity of beam material

I =  moment of inertia of beam section.

Note: In case of calculation of slope  at a point we should apply a unit moment at the specified point of slope and write the equation for m_x

See our solved Problem 7-3 for deflection of beam  by unit load method.

     Pin-jointed Truss

In case of truss the total internal virtual work is obtained by taking the algebraic sum

  

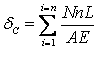
Where,

δ_C = deflection of  joint C

N=axial force in a member due to real loading

n = axial force in the member due to virtual unit load applied at the joint C

L= length of member

A= area of cross-section of the member

E = modulus of elasticity of the member

Note: compressive forces are taken as negative whereas tensile forces are taken as positive.

See our solved Problem 7-5 for deflection of Truss  by unit load method

For other problems please visit our Problem Solver

You can also use our Moment Distribution Calculator for solving indeterminate beams

Use our Fixed Beam Calculator to determine fixed-end moments for different loading cases.