Calculation of Flexural Strength of doubly Reinforced Concrete beam
Problem 9-2
Compute the nominal flexural strength Mn of the
reinforced concrete rectangular section given below in figure
9-2(a). Take fc′ = 5000
psi, width b = 13 in.,
effective depth d = 25 in. The beam has tension steel of As
= 8-#9 bars placed in two layers with a spacing of 1 in. between
them, fy =
40,000 psi, and compression steel of As′
= 2-#8 bars, fs′
= 40,000 psi, effective cover d′ of 3 in.
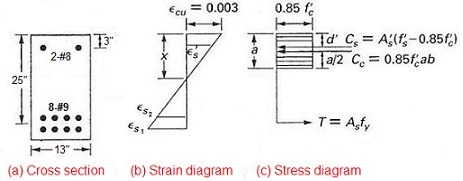
Figure 9-2
Solution:
The given section is doubly reinforced with steel in tension as well as compression zone of the section. The computation of nominal flexural strength Mn is based on the guidelines of ACI-318. The maximum value of usable strain at the extreme concrete fiber is assumed to be 0.003.In the case of two layers of tension steel, the effective depth is taken from the centroid of tension steel to the top edge of the section.
For fc′ grerater than 4000 psi the value of β1 is calculated as given below;
β1 = 0.85 - 0.05 {( fc′ -4000)/1000} = 0.8
Assume that the compression steel has yielded when the strength is reached (strain in concrete is 0.003).
Given that tension steel consists of 8 bars of #9 (dia 1.128 in.) .
Area of one bar of #9 = 1 in2.
As = 8-#9 bars. = 8 (1.00) = 8 in2.
Area of compression steel , As′ = 2-#8 = 2(0.79) = 1.58 in2.
The internal forces acting on the section shown in figure 9-2(c) are calculated as given below;
Cc = 0.85 fc′ ba = 0.85 (5) (13) a = 55.25 a
Cs = (fs′ - 0.85 fc′) As′ = (40 - 0.85*5) 1.58 = 56.485 kips
T = As fy = (8) (40) = 320 kips
Applying static equilibrium, we get Cc + Cs = T;
55.25 a + 56.485 = 320
therefore depth of stress block, a = (320 - 56.485)/55.25 = 4.77 in
Depth of neutral axis x = a / β1 = 4.77/0.8 = 5.96 in
Cc = 55.25 (4.77) = 263.54 kips
By straight line proportion (figure 9-2(b)) we can calculate the strain in compression steel when the extreme concrete fiber has a compressive strain of 0.003.
εs′ = ( x - d′ ) (0.003) / x = (5.96 - 3) (0.003) / 5.96 = 0.00149
yield strain of steel, εy = fy /Es = 40 / 29000 = 0.00138
εs′ is greater than εy , this means that compression steel has yielded before crushing of concrete, hence the assumption is verified and the value of x is valid.
If Compression steel does not yield; then ?? see Example 9-3
Now we determine the strain in the two layers of tension steel.
Using strain diagram we can calculate the strain in tension steel
Lower most layer of tension steel
εs1 = 0.003(25 + 0.5 + 1.28/2 - 5.96) / 5.96 = 0.01
Second layer of tension steel
εs2 = 0.003(25 - 0.5 - 1.28/2 - 5.96) / 5.96 = 0.009
The strain in both the layers of tension steel is more than yield strain and also greater than 0.005. Hence the section is tension-controlled.
The nominal flexural strength is computed as given below; Mn = Cc (d - a/2) + Cs (d - d′ )
= 263.54 (25 - 4.77/2) + 56.485 (25 - 3) = 7202.63 in-kips
Mn = 600.22 ft-kips
see another problem 9-1 and problem 9-3 on Reinforced Concrete
You can also use our
Reinforced concrete calculator for quickly finding the strength of reinforced concrete sections.
You can also use following links of solved examples
Shear force and bending moment diagram for overhanging beam
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Containing Tall building worldwide
Forthcoming conferences
Containing List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
PleaseTell your Friends about us if you find our website useful