Method of sections for Truss member force calculation
Problem 3-2
Using method of sections determine the forces in the members BC, GC and GF of the pin-jointed plane truss shown in figure 3-2(a)
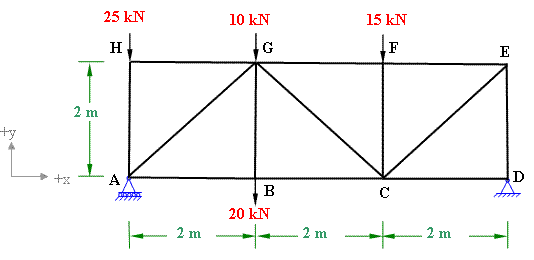
Figure 3-2(a)
Solution:
This truss is determinate as it satisfies the condition of determinacy of plane truss: m = 2j - 3
Reactions at the support:
Support A is on the roller, therefore it will have only vertical reaction and no horizontal reaction. Support D being hinged will experience both horizontal and vertical reactions. (refer to figure 3-2(b)).
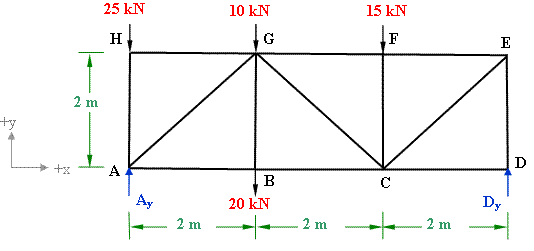
Figure 3-2 (b)
(i) There is no horizontal force acting on the truss therefore the horizontal reaction at D will be zero to satisfy Σ Fx = 0;
(ii) Applying the condition of equilibrium Σ Fy = 0; we get
Ay+ Dy - 25 -10 - 20 - 15 = 0;
Ay+ Dy = 70;
(iii) Σ Mz = 0; Considering z-axis perpendicular to the plane and passing through joint A. Take moment of all the forces about z-axis (taking clock-wise negative and anticlock-wise positive);
Ay x 0 + Dy x 6 - 20 x 2 - 15 x 4 - 10 x 2 + 25 x 0 =0;
we get Dy = 120/6 = 20 kN;
Therefore Ay = 70 - 20 = 50 kN
Calculation of member forces by method of sections
Method of sections is useful when we have to
calculate the forces in some of the members, not all. It is
expalined in this example. We cut the truss into two parts
through section (1) - (1) passing through GF, GC and BC.
We consider the equilibrium of the left side part of the truss as shown in figure
3-2(c).
Figure 3-2(c) While considering equilibrium of this part we look only for
the support reactions, the external forces acting on the
truss, and the member forces which are cut by the section.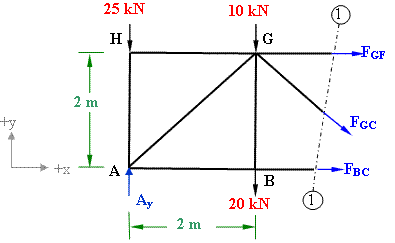
Let's assume the unknown forces in members GF, GC and BC as tensile as shown in the figure.
Σ Fx = 0; => FBC + FGF + FGC cos45 = 0; (i)
Σ Fy = 0; => 50 - 25 - 20 -10 - FGC sin45 = 0; (ii)
FGC sin45 = - 5; FGC = - 7.072 kN;
Σ M = 0 about point G
FBC x 2 - 50 x 2 + 25 x 2 = 0; (iii)
FBC = 25 kN;
Substituting the value of FBC and FGC in eq. (i) we get
FGF = - 20 kN
negative value indicates that the force is opposite to the assumed direction.
| Result of Member forces calculations | ||
| Member | Force (k2N) | Nature of force |
| GC | 7.07 | Compressive |
| BC | 25 | Tensile |
| GF | 20 | Compressive |
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Containing Tall building worldwide
Forthcoming conferences
Containing List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
PleaseTell your Friends about us if you find our website useful