Calculation of slope and deflection by Macaulay's method

Problem 6-1

Use Macaulay's method to determine the values of slope and deflection at 2m from the free end of the cantilever due to the imposed load as shown in figure 6-1(a). The material of beam has modulus of elasticity as 200 GPa. The beam cross-section is T-shaped with flange width as 150 mm and flange thickness 10 mm, web height as 120 mm and web thickness as 8 mm.

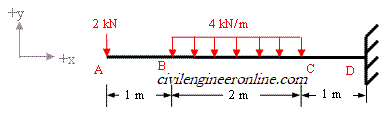
Figure 6-1(a)

Solution:

Because a single equation of bending moment is not able to give values of bending moment at every point of span, We will use Macaulay's Method to find slope and deflection for the above cantilever. The equivalent loading diagram can be drawn as given in figure 6-1(b)

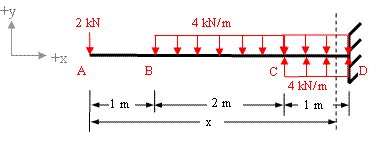
Figure 6-1(b)

The differential equation of elastic curve for this  cantilever can be written as follows;

  EI (d²y/dx²) = -2[x] - 4[x-1][x-1]/2 + 4[x-3][x-3]/2                Eq. 1

Integrating the above equation w.r.t. x  yields;

  EI (dy/dx) = -2[x²/2] - 4[x-1]³/6 + 4[x-3]³/6 + c1             Eq. 2

Apply the boundary condition of slope to find c1;

at x=4, dy/dx=0 because at the fixed support the slope is zero.

=> c1= 16 + 18  - 0.666= 33.33

Substituting the value of c1 into Eq. 2 we get the

  EI (dy/dx) = - 2[x²/2] - 4[x-1]³/6 + 4[x-3]³/6 +33.33

Finally the equation of slope is written as

EI (dy/dx) = - 2[x²/2] - 4[x-1]³/6 + 4[x-3]³/6 +33.33       Eq. 3

and integrating again Eq. 3, we get;

EI y = -2[x³/6] - 4 [x-1]⁴/24 +33.33x +4[x-3]⁴/24 + c2        Eq.4

To get the value of c2 we apply the boundary condition for deflection; because the support at D is fixed and rigid (unyielding) Therefore at x=4, y=0.

Substituting these values of x and y in Eq. 4 we get the value of c2= - 98.5 and the equation for  deflection can be written as

EI y = -2[x³/6] - 4 [x-1]⁴/24 +33.33x +4[x-3]⁴/24 - 98.5    .Eq. 5

Slope at 2m from free end; we put x=2 in Eq.3 (neglect the terms which become negative)

   dy/dx = (28.66)/EI

Deflection at 2m from free end; put  x=2 in Eq. 5 (neglect the terms which become negative)

   y = (- 34.66)/EI

Use moment of inertia calculator for the value of Moment of inertia for T-beam section

 I_xx = 363.76 cm⁴         

  EI= (200x10⁹ N/m²)x(363.76 cm⁴ ) = 727.52 kN m²

Substituting this value of EI in the expressions of slope and deflection we get;

  dy/dx = 28.66/727.52 = 0.0394 rad

   y = - 34.66/727.52 =  - 0.047 m (negative sign indiactes that the deflection is downward)

You can also use our Slope deflection calculator for different combinations of load on cantilever.