Deflection of Truss by unit load method
Problem 7-5
A pin-jointed truss is shown in figure 7-5(a). Determine the vertical displacement of joint E by using unit load method. All the members have cross-sectional area of 250 mm2 and same modulus of elasticity 200GPa.
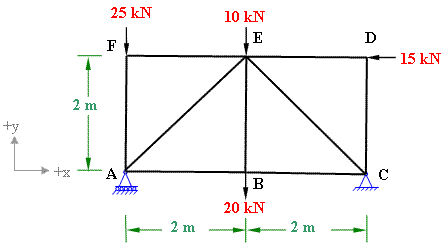
Figure 7-5(a)
Solution:
According to unit load method (also known as virtual work method) the deflection of a joint of truss is given by the following formula
δE = (Σ NnL)/AE
Here we have to find the member forces two times. First we will calculate member forces "N" due to the real loading and then "n" due to unit virtual load applied at the point of required deflection (in this case joint E). Tensile forces are considered as positive and compressive forces as negative. L is the length of the member, A is area of cross-section of the member and E is modulus of elasticity of the material of the truss member.
Step 1: The member forces "N" due to real load are calculated in Example 3-1 .So, we take those values.

Figure 7-5(b)
Step 2: Calculation of member forces "n" due to unit virtual load applied at E as shown in figure 7-5(b).
As the unit load is applied at center of the truss, the support reactions at A and C will be 0.5 kN each.
Considering the equilibrium of joint D, we get FDE =0 and FDC =0;
Similarly the equilibrium conditions at joint F gives;
FFE =0 and FFA =0.
Consider the equilibrium of joint B along y-axis we get FBE =0.
Now consider the equilibrium of joint A.
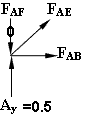
Σ Fy = 0;
FAE sin45 + Ay - FAF = 0 (i)
FAE sin45 + 0.5 - 0 =0
Therefore, FAE = -0.5/sin45 = -0.707 kN
Σ Fx = 0;
FAE cos45 + FAB = 0 (ii)
Therefore, FAB = -FAE cos45 =0.5 kN
As the loading is symmetric, the equilibrium of joint C will also yield the forces similar to the member forces at A
Therefore, FCE = -0.707 kN, FCB = 0.5 kN
All the calculated values are entered in Table 7-5
(In case of mobile device please scroll horizontally to view the full width of table)
| Table 7-5 Result of Member Forces Calculations | ||||
| Member | N (kN) | n (kN) | L (m) | NnL (kN2 m) |
| AB | 22.5 | 0.5 | 2 | 22.5 |
| AF | -25 | 0 | 2 | 0 |
| AE | -31.82 | -0.707 | 2.83 | 63.67 |
| BC | 22.5 | 0.5 | 2 | 22.5 |
| BE | 20 | 0 | 2 | 0 |
| CD | 0 | 0 | 2 | 0 |
| CE | -10.61 | -0.707 | 2.83 | 21.23 |
| DE | -15 | 0 | 2 | 0 |
| EF | 0 | 0 | 2 | 0 |
Σ NnL =129.9 kN2 m
External virtual work = Internal virtual work
1 kN. δE = (Σ NnL)/AE
δE = 129.9/[(250x10-6)(200x106)]
Vertical displacement of Joint E =0.0026 m = 2.6 mm (Ans)
Stress Transformation Calculator
Calculate Principal Stress, Maximum shear stress and the their planes
Calculator for Moving Load Analysis
To determine Absolute Max. B.M. due to moving loads.
Bending Moment Calculator
Calculate bending moment & shear force for simply supported beam
Moment of Inertia Calculator
Calculate moment of inertia of plane sections e.g. channel, angle, tee etc.
Reinforced Concrete Calculator
Calculate the strength of Reinforced concrete beam
Moment Distribution Calculator
Solving indeterminate beams
Deflection & Slope Calculator
Calculate deflection and slope of simply supported beam for many load cases
Fixed Beam Calculator
Calculation tool for beanding moment and shear force for Fixed Beam for many load cases
BM & SF Calculator for Cantilever
Calculate SF & BM for Cantilever
Deflection & Slope Calculator for Cantilever
For many load cases of Cantilever
Overhanging beam calculator
For SF & BM of many load cases of overhanging beam
Civil Engineering Quiz
Test your knowledge on different topics of Civil Engineering
Research Papers
Research Papers, Thesis and Dissertation
List of skyscrapers of the world
Containing Tall buildings worldwide
Forthcoming conferences
Containing List of civil engineering conferences, seminar and workshops
Profile of Civil Engineers
Get to know about distinguished Civil Engineers
Professional Societies
Worldwide Civil Engineers Professional Societies
Keep visiting for getting updated or Join our mailing list
PleaseTell your Friends about us if you find our website useful